Tests gegen die Spezifikation/Anforderungen erstellen: “Blackbox”-Testfälle
https://oer-informatik.de/blackboxtests
https://bildung.social/@oerinformatik/109295949782291326
tl/dr; (ca. 8 min Lesezeit): Die Spezifikation sagt uns vor der ersten Zeile Code eines neuen Programmblocks, wie dieser sich verhalten soll. Wir können im Vorhinein für mögliche Eingabewerte das Resultat unseres Codeblocks bestimmen. Die systematische Ermittlung und Dokumentation dieser Eingabewert/Resultat-Kombinationen durch Äquivalenzklassenbildung und Grenzwertanalyse mündet in “Blackbox”-Testfällen. (Zuletzt geändert am 03.12.2023)
Um systematisch testen zu können sind mehrere Dinge nötig:
Die einzelnen Tests müssen reproduzierbar beschrieben werden. Hierzu gehören vor allem die Eingabewerte eines Tests und das erwartete Resultat. Diese Beschreibungen eines einzelnen Tests nennt man Testfall.
Die jeweiligen Testfälle müssen systematisch ermittelt werden, um eine möglichst gute Testgüte zu erreichen.
Die Testfall-Dokumentation muss nach Durchführen der Tests um die tatsächlichen Resultate ergänzt werden, damit entsprechende Maßnahmen eingeleitet werden können.
Wer diese Punkte beachtet, ist einen entscheidenden Schritt in Richtung Qualitätsmanagement vorangegangen.
Es gibt zwei unterschiedliche Strategien, um Testfälle zu ermitteln:
Blackbox-Ansatz: Testfälle werden aus den Anforderungen/Spezifikation abgeleitet. Man nennt es “gegen die Spezifikation” testen. Hierbei wird die Systematik der Äquivalenzklassenbildung und Grenzwertanalyse angewandt. Diese Testfälle können sogar vor der ersten Zeile Code erstellt werden. Alle, die die Anforderung kennen, können die Blackbox-Systematiken anwenden. Das kann zu jedem Zeitpunkt mit vorliegender Spezifikation erfolgen.
Whitebox-Ansatz: Nach der “Whitebox”-Systematik sind die Anforderungen streng genommen egal. Hier werden Testfälle auf Basis des bestehenden Codes erstellt und es interessiert nur die Testabdeckung: Wird jede Methode/Funktion, Codezeile, Bedingung usw. von den bestehenden Tests erreicht, oder gibt es Bereiche im Code, die bislang nicht von Tests erfasst wurden? Dann müssen Tests für bislang nicht erreichte Codeabschnitte in Kenntnis des Codes erstellt werden. Wir testen also “gegen den Code”.
Daraus ergibt sich eine sinnvolle Reihenfolge in der Testfallerstellung: Wir überprüfen zunächst durch Blackbox-Testfälle, ob die Codeeinheiten den Anforderungen genügt. Im zweiten Schritt überprüfen wir, ob die so erstellten Tests unseren Code komplett (oder in hinreichendem Maß) abdecken und ergänzen ggf. Whitebox-Tests.
Testfalldokumentation
Damit Tests und Ergebnisse reproduzierbar bleiben, müssen alle Testfälle dokumentiert werden. Die Testfalldokumentation kann tabellarisch erfolgen. Häufig muss eine solche Tabelle jedoch nicht selbst geführt werden: die Testframeworks (jUnit, pytest, phpunit…) erstellen diese in ähnlicher Weise selbst. Zur Testfalldokumentation gehören die folgenden Attribute (hier beispielhaft für eine Funktion dividiere(divident, divisor)):
| Testfall Nr. |
Beschreibender Name der Testklasse / des Testfalls | Vor- bedingungen |
Eingabewerte (Parameter divident, divisor) |
Erwartetes Resultat gemäß Spezifikation |
Nach- bedingungen |
Tatsächliches Resultat |
bestanden / nicht bestanden |
|---|---|---|---|---|---|---|---|
| 1. | Ergebnis ist Ganzzahl | keine | divident=8divisor=4 |
2 | - | 2 | ok |
| 2. | Ergebnis ist Gleitkommazahl | keine | divident=1divisor=10 |
0.1 auf sechs signifikante Stellen genau |
- | 0.1 | ok |
| 3. | Teilen durch 0 | keine | divident=1divisor=0 |
UI muss zur Korrektur der Werte auffordern | - | Exception | fail |
Zur Erstellung von Testfällen werden Eingabewerte und Vorbedingungen dokumentiert, erwartete Ausgabewerte und Nachbedingungen können durch das “Testorakel” bestimmt werden. Als Testorakel können i.d.R. die Anforderungen/Spezifikationen herangezogen werden, gegebenenfalls muss hier weiter präzisiert und spezifiziert werden.
Nach Durchführung der Tests wird diese Dokumentation um die Resultate (Ergebnisse, Rückgabewerte) der Tests ergänzt. Außerdem wird noch ein Testergebnis festgehalten: bestanden / nicht bestanden.
Kurzübersicht der beiden Systematiken: Grenzwertanalyse und Äquivalenzklassenbildung
Beim Ermitteln von Testfällen stellt sich schnell die Frage: wie viele Testfälle benötige ich und wie wähle ich geeignete Testfälle aus? Um die Frage zu beantworten wird das erwartete Verhalten und die Eingabewerte betrachtet.
Hierbei stehen zwei Fragen im Vordergrund:
Welche Gruppen von Eingabewerten kann ich bilden, bei denen ich ein ähnliches Verhalten meine Funktion erwarte? Die so ermittelten Gruppen nennen sich Äquivalenzklassen.
Bei welchen Eingabewerten kippt das Verhalten meiner Funktion oder wo verhält sich die Funktion anderweitig besonders? Aus diesen Eingabewerten werden die Grenzwerte ermittelt.
Bei vielen Berechnungen ändert sich das Verhalten unserer Funktionen, wenn wir statt positive Eingabewerte negative verwenden. Wir erhalten beispielsweise bei der oben genannten Divisions-Funktion (dividiere(divident, divisor)) ein negatives Ergebnis, wenn divident oder divisor negativ sind. Es scheint also die Äquivalenzklassen positive Eingabewerte und negative Eingabewerte zu geben.
Andererseits erwarten wir bei der Division bei der 0 und den Grenzen des Definitionsbereichs (z.B. Max.Integer) als Eingabewert ein besonderes Verhalten. Hierbei scheint es sich um interessante Grenzwerte zu handeln, die wir gesondert untersuchen müssen.
An den Rändern der Äquivalenzklassen finden sich häufig Grenzwerte (aber nicht nur dort). Diese beiden Systematiken scheinen sich zu bedingen.

Beispiel: Berechnung von Rabatten
Wenn Funktionen oder Methoden getestet werden, bedeutet das, dass die Signatur (Kopfzeile mit Name, Parameter und Rückgabewert) sowie die Anforderung bekannt sein muss. Um die Systematik der Testfallerstellung kennenzulernen, betrachten wir ein einfaches Beispiel:
Es soll eine Funktion erstellt werden, die Rabatte auf Basis eines übergebenen kosten-Arrays nach folgenden Regeln berechnet: - Beträgt eine Einzelposition (ein Element von kosten) über 100 Euro, so werden 5 Euro Rabatt gewährt - Beträgt die Summe der (rabattierten) Einzelpositionen über 1000 Euro werden zusätzlich 5% Rabatt auf die rabattierte Gesamtsumme gewährt.
Als Eingabewert wird des kosten-Array (eine Liste der Einzelpositionen) übergeben - der Einfachheit halber als Ganzzahl-Array (int[]). Die Funktion soll folgende Signatur haben (Java-Beispiel):
Grenzwertanalyse (Randwertanalyse, Grenzfallanalyse)
Was sind bei der Rabatt-Berechnung diejenigen Werte, bei denen das Verhalten kippt? Es sollten jeweils Testfälle erstellt werden für den Grenzwert sowie (bei Zahlen) die beiden benachbarten Werte.
Grenzwerte von einzelnen Elementen und Eingabewerten
Im Fall der Rabattberechnung betrachten wir zunächst nur einzelne Positionswerte (elemente von kosten). Es gibt den Grenzwert 0, 100 sowie die Bereichsgrenzen, die hier mit Integer.MAX_VALUE und Integer.MIN_VALUE angegeben werden (Java-spezifisch)
Grenzwert Positionswert = 0 oder 1 oder -1:
Grenzwert Positionswert = 100, Positionswert = 101
Positionswert =
Integer.MAX_VALUE,Integer.MAX_VALUE+1, Positionswert =Integer.MAX_VALUE-1Positionswert =
Integer.MIN_VALUE,Integer.MIN_VALUE+1, Positionswert =Integer.MIN_VALUE-1

Grenzwerte von Listen oder Eingabewertkombinationen
Das Verhalten einer Funktion kann sich nicht nur bei einem einzelnen Wert ändern, sondern auch bei einer Kombination verschiedener Eingabewerte. In unserem Beispiel ändert sich das Verhalten, wenn die Summe der Elemente des kosten-Arrays oberhalb von 1000 liegt. Daraus ergeben sich auf für diese Gesamtsumme Grenzwerte:
Grenzwert Gesamtsumme = 0 oder 1 oder -1:
Grenzwert Gesamtsumme = 1000 und 1001
Grenzwert Gesamtsumme =
Integer.MAX_VALUE,Integer.MAX_VALUE+1,Integer.MAX_VALUE-1Grenzwert Gesamtsumme =
Integer.MIN_VALUE,Integer.MIN_VALUE+1, Positionswert =Integer.MIN_VALUE-1
Darüber hinaus ergeben sich auf für die Anzahl der Elemente von kosten Grenzwerte:
Grenzwert leeres Array
kostenGrenzwert
kostenmitInteger.MAX_VALUEElementen (oder die jeweils maximale Anzahl an Elementen)
Zusammenfassen von Grenzwerten, Abwägen der Sinnhaftigkeit
Auch beim Testen muss eine Kosten/Nutzen-Abwägung erfolgen: Welche der genannten Grenzfälle kann mögliche Fehler in der Implementierung aufdecken? Welche Grenzfälle haben hohe Kosten (z.B. Zeit des Testdurchlaufs) bei geringem Nutzen (wenig relevant in der Praxis bzw. geringe Fehlerwahrscheinlichkeit).
Bei den bislang gefundenen Werte stechen hier v.a. die Bereichsgrenzen hervor: ein Array mit der größtmöglichen Anzahl an Elementen (Integer.MAX_VALUE) ist für die allermeisten Anwendungsfälle sicher irrelevant, ein Testlauf wäre sehr aufwändig. Auch die obere und untere Grenze der Positionswerte (bei Integer.MAX_VALUE wären es 2.147.483.647) scheinen in diesem Beispiel wohl wenig relevant. Bedenkt man aber, dass die falsche Wahl eines Datentyps in vielen Programmiersprachen schnell zu einem Überlauf führen kann (z.B. bei Short in Java), erscheint der Test mit einer sehr großen Zahl sinnvoll.
Zusammengefasst ergeben sich folgende Arrays als zu testende Grenzwerte:
- Positionswert und Gesamtsumme 0:
kosten = {0}kosten = {-1}kosten = {1}
- Positionswert 100:
kosten = {100}kosten = {101}
- Gesamtsumme 1000:
kosten = {1000}kosten = {1001}
- leeres Array:
kosten = {}
Dazu kommen - nach Abwägung - die Grenzwerte am Rand des Definitionsbereichs
- Grenzen des Definitionsbereichs:
kosten = {Integer.MAX_VALUE}kosten = {Integer.MAX_VALUE-1}kosten = {Integer.MAX_VALUE+1}sofern dies in der jeweiligen Programmiersprache umsetzbar istkosten = {Integer.MIN_VALUE}kosten = {Integer.MIN_VALUE+1}kosten = {Integer.MIN_VALUE-1}sofern dies in der jeweiligen Programmiersprache umsetzbar ist
Allgemein: Typische Grenzwerte
Bei der Grenzwertanalyse ist die schwierige Aufgabe, die spezifikationstypischen Grenzwerte zu ermitteln - insbesondere, wenn diese aus einer Kombination der Eingabewerte bestehen. Darüber hinaus gibt es aber eine Reihe von Grenzwerten, die unabhängig von der konkreten Spezifikation häufig Probleme hervorrufen - und abhängig vom verwendeten Datentypen sind.
Auch hier gilt: es ist vorher abzuwägen, ob die theoretisch ermittelten Grenzwerte auch praktische Relevant haben - und ob das Aufwand/Nutzen Verhältnis für die Grenzwerte stimmt.
Bei Zahlentypen
Die Werte für Ganzzahlen haben wir oben bereits analysiert: untere Grenze, obere Grenze und 0 - sowie jeweils den Wert +/-1. Bei Festkommazahlen (wie z.B. Decimal in vielen Datenbankmanagementsystemen) gelten die gleichen Werte - nur eben um die feste Anzahl der Nachkommastellen verschoben.
Besonders bei Ganzzahlentypen ist es wichtig, die Werte rechts und links des Grenzwerts zu testen, da “Off-By-One-Errors” (OBOE) zu den häufigsten Fehlerquellen zählen.
Bei Gleitkommazahlen ist es etwas schwieriger: die obere und untere Grenze lässt sich häufig analog zu Int in einer Programmiersprachen-Konstanten finden. Aber schwieriger ist es, die direkten Nachbarwerte dieser Grenzwerte zu bestimmen. Viele Programmiersprachen bieten hierfür eigene Funktionen an (in Java etwa Math.nextDown() / Math.nextUp()). Häufig ist es jedoch gar nicht erforderlich, den direkten Nachbarwert der Grenzen zu ermitteln, sondern es langt einen hinreichend nahen Wert über und unter der Grenze zu testen.
Im Fall von Java wären potenzielle Grenzwerte:
Double.MIN_VALUE(kleinste darstellbare positive Zahl, mit geringerer Präzision)Double.MIN_NORMAL(kleinste mit normaler Präzision darstellbare positive Zahl - größer alsDouble.MIN_VALUE)Double.MAX_VALUE(die größte darstellbare Zahl)- Double.MAX_VALUE(die kleinste darstellbare Zahl)Double.MIN_NORMAL(kleinste mit normaler Präzision darstellbare positive Zahl - größer alsDouble.MIN_VALUE)
Diesseits des Definitionsbereichs beitet Java beispielsweise die Konstanten:
Double.NEGATIVE_INFINITYDouble.POSITIVE_INFINITYDouble.NaN
Bei Objekten
Erfahrungsgemäß ist der eine der häufigsten Fehlerquellen die NullPointerException. In jedem Fall sollte bei allen Objekten das Verhalten definiert sein, falls kein Objekt übergeben wurde: * NULL, None oder wie auch immer die Bezeichnung in der jeweiligen Programmiersprache ist.
Bei Objektsammlungen
Auch Objektsammlungen hatten wir bereits angesprochen. Bei Sets, Maps (Dictionaries) und Listen (Arrays) sollten immer getestet werden:
kein Element
ein
NULLElementbei nicht generischen Arrays: ein Element falschen Typs
ein Array mit der Maximalen Anzahl an Elementen
Bei Zeichenketten:
Leerstring ""
Leerzeichen " "
Randbedingungen beachten
Die hier getroffenen Feststellungen gelten nicht nur für die Parameter oder direkten Eingabewerte, sondern ggf. genauso für Randbedingungen der Testfälle.
Äquivalenzklassenmethode
Es ist in der Regel nicht sinnvoll und zumeist auch unmöglich alle auftretenden Werte zu testen. Die Äquivalenzklassenmethode besagt, dass alle Bereichen, in denen wir ein gleichwertiges Verhalten erwarten, mindestens mit einem Testfall abgedeckt werden müssen.
Äquivalenzklassen zwischen Grenzwerten
Mit der Grenzwertbetrachtung haben wir bereits viele Werte definiert, an denen sich das Verhalten unserer Funktion/Methode ändert. Häufig verhalten sich Funktionen mit Eingabewerten zwischen benachbarten Grenzwerten ähnlich, so dass wir mit der Grenzwertanalyse auch unmittelbar Kandidaten für Äquivalenzklassen gefunden haben.
Auf unser Rabattbeispiel trifft dies auch zu: wir erwarten von kosten = {10} ein ähnliches Verhalten wie von kosten = {47}.

Damit für unser Beispiel jede Äquivalenzklasse einmal getestet wird (über die Grenzwerte hinaus) wählen wir also aus:
Äquivalenzklasse gültige Einzelpositionswerte:
ÄK kein Rabatt auf Einzelposition:
kosten = {50}
ÄK Rabatt auf Einzelposition:
kosten = {300}
Falls in den Anforderungen ein Definitionsbereich für Eingabewerte festgelegt ist, haben wir noch die ÄK ungültige Werte, hier beispielsweise negative Einzelpositionen:
Äquivalenzklasse ungültige Werte:
kosten = {-50}
Weiterhin gibt es noch die Äquivalenzklassen, die sich aus der Gesamtkostenrabattierung zwischen den Grenzwerten ergeben:

Äquivalenzklasse gültige Gesamtsumme:
ÄK kein Rabatt auf Gesamtsumme:
kosten = {50}(kann identisch zu “kein Rabatt auf Einzelposition” gewählt werden)
ÄK Rabatt auf Gesamtsumme:
kosten = {2000}
Falls in den Anforderungen ein Definitionsbereich für Eingabewerte festgelegt ist, haben wir noch die ÄK ungültige Werte, hier beispielsweise negative Einzelpositionen:
Äquivalenzklasse ungültige Werte:
kosten = {-50}(kann identisch zu “kein Rabatt auf Einzelposition” gewählt werden)
Äquivalenzklassen unabhängig von Grenzfällen
Doch schon beim Divisionsbeispiel (dividiere(divident, divisor)) müssen wir weitere Äquivalenzklassen bilden:
Der Aufruf dividiere(8, 2)==4 verhält sich grundlegend anders als dividiere(8,3)==2 (bei ganzzahliger Division ohne Rest). Es gibt also Äquivalenzklassen, die nicht sortiert am Zahlenstrahl eines Eingabewerts zwischen Grenzwerten vorzufinden sind, wie unsere bisherigen Beispiel. Häufig ist es in solchen Fällen erst eine Kombination bestimmter Parameter, die ein besonderes Verhalten hervorruft.
Hier ist gutes Gespür und viel Erfahrung von Nöten, um diese Art der Äquivalenzklassen aus der Spezifikation herauszulesen.
Allgemein: mögliche Äquivalenzklassen
Wenn alle Äquivalenzklassen zwischen Grenzwerten bestimmt sind und die Spezifikation auf weitere Äquivalenzklassen hin untersucht wurde, kann noch die folgende Liste als Anhaltspunkt und Ideengeber für weitere Äquivalenzklassen herhalten:
Unterschiedliche Arten gültiger Eingabewerte
Unterschiedliche Arten ungültiger Eingabewerte (wurde in den Anforderungen festgelegt, wie sich das System verhalten soll?):
Überschreitung des gültigen Definitionsbereichs für einen Eingabewert
Unterschreitung des gültigen Definitionsbereichs für einen Eingabewert
positive und negative Eingabewerte
Eingabewerte, bei denen ein positives und negatives Ergebnis erwartet wird
ganzzahlige Eingabewerte
Gleitkomma Eingabewerte
Festkomma Eingabewerte (Rundungsfehler durch Binärabbildung von Double einkalkuliert?)
Zeichenketten mit ASCII-Buchstaben, ASCII-Steuerzeichen, Zahlen, Leerzeichen
Zeichenketten mit UNICODE-Sonderzeichen, mit fehlimportierten Zeichencodierungen
Zeichenketten mit den unterschiedlichen OS-typischen Kombinationen aus Newline und Linefeed
Zeichenketten mit HTML-Formatierung statt plain/text
…
Wahl und Zusammenfassung von Äquivalenzklassen
Wurden neben den Äquivalenzklassenkandidaten zwischen den Grenzwerten weitere neue Äquivalenzklassen gefunden und gebildet, so sollte nochmals überprüft werden, ob auch deren Grenzen bei den Grenzwert-Testfällen vorhanden sind (und ggf. ergänzt werden).
Aus jeder Äquivalenzklasse sollte mindestens ein Testfall erstellt werden. Es bietet sich an, diesen mit üblichen Eingabewerten zu versehen (sonst ggf. aus der Mitte der Äquivalenzklasse). Zusätzlich mit den beiden Testfällen an den Grenzen der Äquivalenzklasse (die aus der Grenzwertanalyse stammen) sollte somit eine gute Abdeckung vorhanden sein, die viele potenzielle Fehler finden kann.
Es gilt im Anschluss die gleiche Aufwand/Nutzen-Betrachtung wie bei den Grenzfällen: welche Äquivalenzklassen haben praktische Relevanz? Bei welchen steht der (Rechen-/Speicher-)Aufwand in keinem Verhältnis zum erwarteten Nutzen?
Aus der Fülle der möglichen Testfälle gilt es, eine representative, Effiziente und angemessene Testfallsuite zusammenzustellen.
Kombination der ermittelten Testfälle
Die so identifizierten Eingabewerte und Randbedingungen unserer unterschiedlichen Äquivalenzklassen können miteinander wechselwirken. Es wäre daher wünschenswert, nicht nur jede Äquivalenzklasse einmal zu testen, sondern auch jede Kombination von Äquivalenzklassen unterschiedlicher Eingabewerte. Bereits die Kombination von wenigen Eingabewerten (und Randbedingungen) mit wenigen Äquivalenzklassen führt zu unübersichtlich vielen Testfällen. Selbst in unserem einfachen Bespiel führt die Unterscheidung, ob Grenzen in einem oder mehreren Werten überschritten werden - und ob ein oder mehrere Werte ungültig sind zu einer Vielzahl von Testfällen, ein paar Beispiele sind hier dargestellt:

Um die Anzahl der Testfälle einzugrenzen - und um die Übersicht zu erhalten - werden nicht alle möglichen Kombinationen getestet. Es gibt verschiedene Techniken (und Software) auf dem Markt, die hilft die Vielzahl möglicher Testfall-Kombinationen ohne großen Verlust der Testgüte reduziert. Als Mindestvoraussetzung der Kombination von Äquivalenzklassen gelten:
Alle Grenzfälle zwischen Äquivalenzklassen sollten einmal getestet werden.
Jede Äquivalenzklasse muss mindestens einmal getestet werden. Wenn möglich sollte jede paarweise Kombination aus Äquivalenzklassen einmal getestet werden.
Eine Äquivalenzklasse mit ungültigen Eingabewerte darf nur mit Äquivalenzklassen mit gültigen Eingabewerten kombiniert werden.
Bei komplexeren Testobjekten hilft es, diese Kombinatorik beispielsweise mit Hilfe der Klassifikationsbaummethode zu planen.
Fazit
Die Testfallerstellung mit Blackbox-Systematik hilft zum einen, die Anforderungen und Spezifikation genau zu verstehen, deren Einhaltung zu prüfen und deren Details zu dokumentieren. Lücken in der Spezifikation werden auf diesem Weg aufgedeckt ebenso wie Verständnisprobleme auf beiden Seiten.
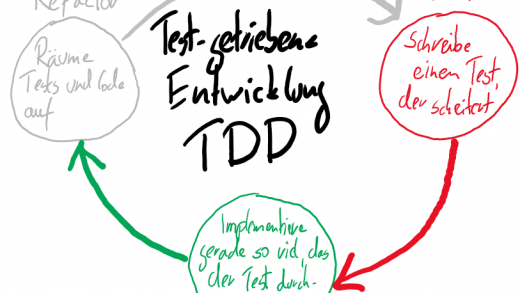
Da Blackbox-Tests bereits vor der eigentlichen Implementierung erstellt werden können, können sie zudem dabei helfen, das große Gesamtproblem in kleine Einzelprobleme zu unterteilen, die jeweils für sich leichter zu lösen sind. Dieser Ansatz ist in der Testgetriebenen Entwicklung (TDD) umgesetzt.
Blackbox-Tests eignen sich auf allen Ebenen der Programmierung: Als Unit-Test für kleine Codeeinheiten, als Integrationstests, im Zusammenspiel mehrerer Codeeinheiten und als System- oder Abnahmetest für das Gesamtprojekt.
Essenziell ist eine Dokumentation, die für eine Reproduzierbarkeit der Test sorgt. Von unermesslichem Vorteil ist eine Automatisierung der Blackbox-Tests.
Übungsaufgaben (Blog-Eintrag auf oer-informatik.de)
Links, Literatur und Quellen
Testgetriebene Entwicklung (mit pytest) (Blog-Eintrag auf oer-informatik.de)
Whitebox-Testfallerstellung auf Basis von Code-Coverage Analyse (Blog-Eintrag auf oer-informatik.de)
Das Standardwerk des Softwaretestens ist “Basiswissen Softwaretest” von Andreas Spillner und Tilo Linz, dPunkt Verlag, Heidelberg, ISBN 978-3-86490-024-2
Hinweis zur Nachnutzung als Open Educational Resource (OER)
Dieser Artikel und seine Texte, Bilder, Grafiken, Code und sonstiger Inhalt sind - sofern nicht anders angegeben - lizenziert unter CC BY 4.0. Nennung gemäß TULLU-Regel bitte wie folgt: “Tests gegen die Spezifikation/Anforderungen erstellen: "Blackbox"-Testfälle” von Hannes Stein, Lizenz: CC BY 4.0. Der Artikel wurde unter https://oer-informatik.de/blackboxtests veröffentlicht, die Quelltexte sind in weiterverarbeitbarer Form verfügbar im Repository unter https://gitlab.com/oer-informatik/qs/blackboxtest. Stand: 03.12.2023.
[Kommentare zum Artikel lesen, schreiben] / [Artikel teilen] / [gitlab-Issue zum Artikel schreiben]