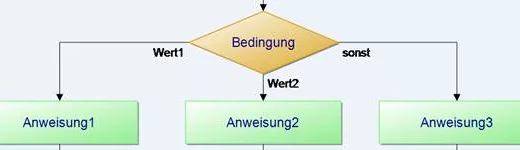
Metrik der Komplexität eines Algorithmus: Die McCabe-Zahl (Zyklomatische Komplexität)

Metrik der Komplexität eines Algorithmus: Die McCabe-Zahl (Zyklomatische Komplexität)

https://bildung.social/@oerinformatik/

https://oer-informatik.de/zyklomatische-komplexitaet

Zyklomatische Komplexität, McCabe-Zahl, Softwaremetriken, Kontrollflussgraph, Basispfade, Whitebox-Test, Testbarkeit, Wartbarkeit, Refaktorisierung, JaCoCo

tl/dr; (ca. 15 min Lesezeit): Die Zyklomatische Komplexität (McCabe-Zahl) gibt ein Maß für die Wartbarkeit von Code an. Sie kann auf verschiedene Arten bestimmt werden (binäre Verzweigungen, Anzahl Pfade, Anzahl Knoten und Kanten). Sie kann als Indikator für zu hohe Komplexität innerhalb von Methoden genutzt werden, kann aber objektorientierte Komplexität nicht detektieren [AI-Assisted]. (Zuletzt geändert am 23.10.2026)

Dieser Artikel ist Teil einer Artikelreihe über die Komplexität von Algorithmen: Laufzeitkomplexität und Big-O-Notation / Zyklomatische Komplexität (McCabe-Zahl) / Zyklomatische Komplexität von Bubblesort

Schon fit in diesem Thema? Nutze die Kann-Liste und die Leitfragen unter dem Artikel als Checkliste, ob Du die relevanten Kompetenzen bereits hast. Hier klicken, um Kann-Liste ein- oder auszublenden

Zu den Qualitätsanforderungen von Software gehört es, dass diese testbar, wartbar und evolvierbar (erweiterbar) sein soll. Wie können wir nachweisen, dass unsere Software diesen Anforderungen genügt?

Welche Metriken zur Messung der Komplexität von Software gibt es?

Wartbarkeit, Testbarkeit und Erweiterbarkeit von Software sind nicht direkt messbar, die Beurteilung erfolgt oft sehr subjektiv. Zu einer fachgerechten Anforderungsanalyse gehört es aber, überprüfbare und möglichst objektivierte Anforderungen zu formulieren (vgl. S.M.A.R.T.-Methodik im Projektmanagement bzw. I.N.V.E.S.T.-Methodik für Backlog-Items). Daher wurden Metriken (Kennziffern) entwickelt, die messbare Indikatoren nutzen, um Qualitätsmerkmale wie Wartbarkeit, Testbarkeit und Erweiterbarkeit von Software mittelbar (also über Umwege) zu beschreiben. Die Komplexität von Software ist ein solcher Indikator: je komplexer ein Softwaremodul ist, desto schwieriger ist es testbar, wartbar und erweiterbar. Doch Komplexität selbst ist auch keine objektiv messbare Größe. Man hilft sich daher mit unterschiedlichen Metriken aus, die zumeist von der Entwicklungsumgebung direkt bereitgestellt werden:

• Lines of Code (LoC): Die Anzahl der Codezeilen gibt das einfachste Maß für den Umfang eines Projekts. Über die Komplexität ist die Aussagekraft allerdings begrenzt.
• Objektorientierte Metriken gehen tiefer auf komplexe Strukturen ein:
  • Attributbasierte Metriken nutzen die Anzahl der Felder/Member einer Klasse:
    • Number of Variables (NoV): Die reine Anzahl der Instanzvariablen eines Objekts gibt ein gutes erstes Maß wieder.
    • Lack of Cohesion of Methods (LCOM): Mit dieser Metrik wird ermittelt, wie viele Instanzvariablen von unterschiedlichen Methoden gemeinsam benutzt werden - wie stark Methoden also zusammenhängen (sich überdecken in den genutzten Objekten/Werten).
  • Methodenbasierte Metriken:
    • Number of Methods (NoM): Anzahl der Methoden einer Klasse
  • Vererbungsspezifische Metriken:
    • Number of Children (NoC): Wie oft wurde von einer Klasse geerbt?
    • Depth of Inheritance Tree (DIT): Länge des Vererbungspfads von einer Klasse bis zur Wurzel der Vererbungshierarchie
    • Number of Redefined Methods (NORM): Anzahl der überschriebenen Methoden einer erbenden Klasse

Die Aussagekraft dieser Metriken ist oft nur im Zusammenhang erschließbar, so dass es hier keine allgemeingültigen Grenzwerte für zu komplexe Software gibt.

Ein weiterer Indikator auf Methoden/Funktionsebene ist die Anzahl der unterschiedlichen Wege, die durch eine Methode genommen werden kann. Mit jeder bedingten Anweisung oder Schleife kann der Programmablauf (Kontrollfluss) unterschiedliche Operationen erreichen.

Ein Maß für die Anzahl unterschiedlicher Wege durch eine Methode - wir sprechen von Pfaden - nennt man Zyklomatische Komplexität. Sie wird nach Thomas McCabe häufig auch McCabe-Zahl genannt und mit M abgekürzt.

Die Zyklomatische Komplexität gibt an, wie viele Testfälle wir benötigen, um alle linear unabhängigen Pfade (Basispfade) einer Methode einmal zu durchlaufen. Um jede Kante (jeden Zweig) mindestens einmal zu durchlaufen, reichen höchstens so viele Testfälle – oft weniger.

Kontrollflussgraph einer Methode

Um unterschiedliche Pfade durch einen Codeblock / eine Methode zu identifizieren, muss zunächst der Kontrollfluss bestimmt werden. Das geht über den Kontrollflussgraphen am nachvollziehbarsten:

• Ein Kontrollflussgraph hat einen Einstiegspunkt und einen Ausstiegspunkt der Methode.

• Unverzweigte Operationssequenzen können zu einem Knoten zusammengefasst werden.

• Verzweigungen (Bedingte Anweisungen, Schleifen) werden durch mehrere ausgehende Kanten dargestellt.

• Jeder Knoten kann mehrere eingehende Kanten haben.

Ein einfacher Kontrollflussgraph kann beispielsweise so aussehen:

Abgebildet ist der Kontrollfluss einer Methode. Die Methode hat einen Einstiegspunkt (Start) und einen Ausstiegspunkt (Stop). Jeder Knoten (1-7) steht für eine unverzweigte Programmsequenz. Die Kanten (Pfeile) stellen mögliche Übergänge zwischen unterschiedlichen Programmsequenzen dar:

• eine Schleife / ein Rücksprung: (6) -> (1)
• eine bedingte Anweisung ohne Alternative (if): (3) -> (4) -> (5) bzw. (3) -> (5)
• eine bedingte Anweisung mit Alternative (if/else): (2) -> (7) -> (5) bzw. (2) -> (3)... -> (5)

Zum weiteren Verständnis ist es nicht unbedingt erforderlich, Quelltext für den Kontrollfluss vor Augen zu haben. Falls es doch das Verständnis unterstützt: ein Java-Quellcodebeispiel könnte etwa die Methode zaehle(von, bis) sein:

public static void zaehle(int von, int bis){
  do{
    if (von == 1){
      System.out.println("Wir fangen mit 1 an");
    }else{
      System.out.print(von);
      if (von<bis){
        System.out.println(" und noch eine Runde");
      }
    }
    von++;
  }while (von <= bis);
}

Bestimmung der Zyklomatischen Komplexität über binäre Verzweigungen

Die Anzahl der “linear unabhängigen Pfade” durch eine Methode (also die Zyklomatische Komplexität) lässt sich oft am einfachsten über die Anzahl der binären Verzweigungen b bestimmen. Die Zyklomatische Komplexität ist die Anzahl der binären Verzweigungen plus eins:

M = b + 1

Binäre Verzweigungen sind alle Verzweigungen mit genau zwei ausgehenden Kanten. In unserem Beispiel gibt es an den Knoten (2) (mit den ausgehenden Kanten b und g), (3) (mit den ausgehenden Kanten c und f) sowie am Knoten (6) (Kanten i und die Kante x zum Methodenende!!!) binäre Verzweigungen:

Bei drei gezählten binären Verzweigungen ergibt sich die Zyklomatische Komplexität zu:

M = b + 1 = 3 + 1 = 4

Sofern im Kontrollfluss Verzweigungen mit mehr als zwei alternativen Zweigen auftreten, müssen diese in binäre Verzweigungen umgerechnet werden. Beispielhaft ist folgender Kontrollfluss mit einer Verzweigung mit vier Zweigen gegeben (z.B. ein switch/case nach den vier Jahreszeiten):

Bei Umwandlung in binäre Verzweigungen entsteht genau eine binäre Verzweigung (b) weniger, als die Verzweigung Alternativzweige (z) hatte.

b = z - 1

Eine Verzweigung mit 4 Alternativen lässt sich also in 3 binäre Verzweigungen umwandeln (bspw.: switch/case in if/else umwandeln). Mit diesem Wert lässt sich wiederum die Zyklomatische Komplexität bestimmen.

Bestimmung der Zyklomatischen Komplexität über die linear unabhängigen Pfade

Da für die Zyklomatische Komplexität (oder McCabe-Zahl) M gilt:

M = Anzahl\ linear\ unabhängiger\ Pfade

Wann ist ein Pfad linear unabhängig? Voneinander linear unabhängig sind Pfade, wenn sie jeweils mindestens eine Kante durchlaufen, die die anderen Pfade nicht durchlaufen.

In unserem relativ einfach gehaltenen Beispiel lassen sich noch recht schnell manuell vier Pfade identifizieren:

Pfad 1: Start -> (1) -> (2) -> (3) -> (4) -> (5) -> (6) -> Stop

Pfad 2 mit Alternative in (2): Start -> (1) -> (2) -> (7) -> (5) -> (6) -> Stop

Pfad 3 mit Alternative in (3): Start -> (1) -> (2) -> (3) -> (5) -> (6) -> Stop

Pfad 4 mit Rücksprung: Start -> (1) -> (2) -> (3) -> (4) -> (5) -> (6) -> (1 - Wiederholung)

Wichtig ist bei Wiederholungen, dass die Pfade nur bis zum ersten wiederholten Knoten betrachtet werden. Ein zweiter Durchlauf wird bei der Prüfung linearer Unabhängigkeit nicht durchgeführt.

Wir erhalten an Hand des Kontrollflusses vier linear unabhängige Pfade.

M = Anzahl\ linear\ unabhängiger\ Pfade = 4

Kontrollflussgraphen betrachten die eigentlichen Bedingungen an den Verzweigungen nicht. Durch Abhängigkeiten dieser Bedingungen ist es jedoch möglich, dass im eigentlichen Programmfluss einige Zweig-Kombinationen nicht auftreten können. In unserer Beispielmethode zaehle() tritt die Bedingung (von<bis) immer mit der Bedingung (von <= bis) auf - die Kanten f und i sind also voneinander abhängig. Für die Berechnung der Zyklomatischen Komplexität werden solche Abhängigkeiten jedoch nicht beachtet!

Bestimmung der Zyklomatischen Komplexität über Knoten und Kanten des Kontrollflusses

Die Zyklomatische Komplexität lässt sich auch aus den Kanten (edges, e) und Knoten (nodes, n) des Kontrollflussgraphen berechnen. Im einfachsten Fall kann sie wie folgt berechnet werden:

M = e - n + 2

Im Ausgangsbeispiel zählen wir sieben Knoten plus Start plus Stop (n=9) und neun Kanten zzgl. Start und Ende (e=11) - die Kante von “Stop” zu “Start” nicht mitgezählt.

M = 11 - 9 + 2 = 4

Die 2 am Ende ist eine Vereinfachung, die wir anwenden können, wenn wir nur eine unabhängige Methode betrachten. Sie steht eigentlich für 1 + p: die 1 für die in der Regel nicht eingezeichnete Rücksprungkante von Stop zu Start (oben als e12 eingezeichnet). p steht für die Anzahl unabhängiger Kontrollflussgraphen, die gemeinsam untersucht werden. In der Praxis ist p für Methoden daher i.d.R. 1. In der Literatur finden sich Formeln, die von anderen Voraussetzungen ausgehen (z.B. Mitzählen der Rücksprungkante). In den folgenden Beispielen werden die oben genannten Voraussetzungen genutzt, die Formel lautet demnach:

M = e - n + 2

Wichtig ist hierbei zu beachten, dass der Kontrollflussgraph genau einen Einstiegspunkt und einen Ausstiegspunkt hat - evtl. müssen also die Kanten mehrerer Ausstiegspunkte (z.B. mehrerer return-Statements) noch zusammengeführt werden, um die Berechnung korrekt durchzuführen.

Ein weiteres Beispiel zur Ermittlung der Zyklomatischen Komplexität von BubbleSort findet sich im Artikel Die Zyklomatische Komplexität des Bubblesort-Algorithmus.

Tools zur Erstellung von Metriken

Die manuelle Berechnung der Zyklomatischen Komplexität ist natürlich mühsam und wenig praxistauglich.

Diese Aufgabe sollte am besten von Frameworks übernommen werden, die sich auch um andere Metriken kümmern. In der Regel gibt es für die xUnit-Frameworks Plugins, die neben der Codeabdeckung der Tests auch die Zyklomatische Komplexität berechnen. Bei Java ist beispielsweise JaCoCo oder EclEmma zu empfehlen. Die Berichte erfolgen dann auf Methodenbasis:

Im obigen Bericht sieht man, dass in der Klasse AddressController lediglich die Methode put() über eine nennenswerte Logik verfügt (M = 11, ausgegeben in der Spalte Cxty) - bei den anderen Methoden scheint es sich mehr oder weniger um sequenzielle Integrations- oder Operationsmethoden zu handeln (M=1, M=2).

Aktuelle Aussagekraft der Zyklomatischen Komplexität

Die Zyklomatische Komplexität hat ihren Ursprung in der Zeit der strukturierten Programmierung, weswegen ihr bisweilen mangelnde Aussagekraft in aktuellen Projekten nachgesagt wird.

Zyklomatische Komplexität und switch/case

Es wird häufig angeführt, dass die empfundene Komplexität von Codeblöcken – vor allem bei switch/case-Konstrukten – deutlich geringer ist, als es die McCabe-Zahl vermuten lässt. Eine Aufteilung nach Wochentagen per switch/case wird hier häufig genannt:

M = 16 - 11 + 2 = 7

Für Menschen ist das leicht verständlich, dieser einfache Kontrollfluss hat aber eine McCabe-Zahl von M=7.

Diese Kritik ist berechtigt, wenn es um die Evolvierbarkeit von Code geht: hier sind switch/case-Konstrukte für Programmierende tatsächlich wenig komplex. Aus Sicht des Testens jedoch bleibt die Aussagekraft der McCabe-Zahl auch hier erhalten. Sie bleibt Indiz, aber nicht Beweis für komplexe Systeme.

Zyklomatische Komplexität und der implizite Kontrollfluss der Objektorientierung

Weiterhin wird häufig aufgeführt, dass mit Hilfe der Zyklomatischen Komplexität zwar explizit implementierter Kontrollfluss erfasst wird (bedingte Anweisungen, Wiederholungsstrukturen) - in objektorientierten Sprachen jedoch häufig ein impliziter Kontrollfluss über Polymorphie, Lambda-Ausdrücke oder ähnliches erfolgt, den die McCabe-Zahl nicht erfasst.

Als Beispiel: Mithilfe der Stream-API und Lambda-Ausdrücken lassen sich in Java Objektströme erzeugen, filtern, abbilden und ausgeben (filter-map-reduce). Hier werden alle geraden natürlichen Zahlen zwischen 1 und 7 ausgegeben:

java.util.stream.IntStream.range(1, 7).filter(a->(a%2==0)).forEach( System.out::println );

Der implizite Kontrollfluss erstellt hier Objekte, übergibt Methodenimplementierungen, durchläuft Schleifen und ist nicht trivial in einem Kontrollflussgraph darstellbar. Explizit wird eine Operation aufgerufen - ggf. werden noch drei Operationen identifiziert:

IntStream zahlenstrom = IntStream.range(1, 7);
zahlenstrom = zahlenstrom.filter(a->(a%2==0));
zahlenstrom.forEach( System.out::println );

… aber die Komplexität der bedingten Anweisung (a%2==0) und des Aufrufs jedes Stream-Objekts analog zu einer Iteration forEach( System.out::println ) wird im expliziten Kontrollfluss nicht abgebildet.

Hier liegt die wohl größte Schwäche dieser Metrik. Sie erfasst nur einen Teil der eigentlichen Komplexität und darf somit nicht als alleiniges Maß für Komplexität verwendet werden.

Jedoch bildet sie einen Teil der durch Programmierende beeinflussbaren Komplexität ab. Denn ein großer Teil der Komplexität, die über Funktionale Programmierung oder Polymorphie in den Kontrollfluss eines Softwaremoduls gelangt, liegt nicht mehr im Einflussbereich einzelner Programmierender, sondern findet auf Framework- oder Compiler/Interpreter-Ebene statt.

In objektorientierten oder funktionalen Projekten ist die Aussagekraft der Zyklomatischen Komplexität also mit Vorsicht zu genießen, bleibt aber ein wichtiger Indikator für potenzielle Probleme im strukturellen Design von Methoden.

Einordnung der Werte Zyklomatischer Komplexität

Es gibt hier keine allgemeingültige Antwort, ab welchem Wert der Zyklomatischen Komplexität eine Methode zu komplex ist und unterteilt oder refaktorisiert werden sollte. Da die Zyklomatische Komplexität ein Maß dafür ist, wie viele Testfälle wir pro Methode benötigen, darf angenommen werden, dass das Fehlerrisiko mit größerem Wert der Zyklomatischen Komplexität steigt, während die Evolvierbarkeit in gleichem Maß sinkt. In der Literatur finden sich häufig die folgenden Grenzen:

• M ≤ 10: Die Methode ist gut testbar und wenig komplex. Dieser Bereich sollte angestrebt werden.

• 11 ≤ M ≤ 20: Die Methode ist noch testbar und mit vertretbarem Aufwand erweiterbar. Sofern es sich um sicherheitsrelevante Methoden handelt, sollte bereits hier erwogen werden, ob die Testbarkeit nicht durch Refaktorisierung erhöht werden kann.

• 21 ≤ M ≤ 50: Die Methode ist komplex, daher kaum erweiterbar und schwer zu testen. Wenn möglich sollte zu Refaktorisierungs-Methoden gegriffen werden, um die Komplexität zu senken. In jedem Fall sollten sicherheitsrelevante Methoden einer Refaktorisierung unterzogen werden.

• M > 50: Solche Methoden gelten als untestbar und nicht erweiterbar. Diese Methoden sollten auf jeden Fall einer Refaktorisierung unterzogen werden, da die Fehlerwahrscheinlichkeit sehr hoch ist.

Leitfragen

1. Warum werden Metriken wie die Zyklomatische Komplexität genutzt, um Software zu beurteilen? Antwort

Testbarkeit, Wartbarkeit und Erweiterbarkeit lassen sich nicht direkt messen. Metriken wie Lines of Code, objektorientierte Metriken oder die Zyklomatische Komplexität beschreiben sie mittelbar über messbare Indikatoren: Je komplexer ein Modul, desto schwerer ist es zu testen, zu warten und zu erweitern, siehe Abschnitt „Welche Metriken zur Messung der Komplexität von Software gibt es?“.

2. Wie ist ein Kontrollflussgraph aufgebaut? Antwort

Er hat genau einen Einstiegs- und einen Ausstiegspunkt. Unverzweigte Anweisungsfolgen werden zu einem Knoten zusammengefasst, Verzweigungen und Schleifen erscheinen als Knoten mit mehreren ausgehenden Kanten, und jeder Knoten darf mehrere eingehende Kanten haben, siehe Abschnitt „Kontrollflussgraph einer Methode“.

3. Wie bestimmst Du die Zyklomatische Komplexität über binäre Verzweigungen, und wie gehst Du mit einem switch/case mit vier Zweigen um? Antwort

Du zählst die binären Verzweigungen b und rechnest M = b + 1. Eine Verzweigung mit z Zweigen entspricht z - 1 binären Verzweigungen, ein switch/case mit vier Zweigen also drei, siehe Abschnitt „Bestimmung der Zyklomatischen Komplexität über binäre Verzweigungen“.

4. Wie berechnest Du die Zyklomatische Komplexität aus Knoten und Kanten? Antwort

Mit M = e - n + 2, wobei e die Kanten und n die Knoten des Kontrollflussgraphen einer Methode mit genau einem Ein- und Ausstiegspunkt sind (Rücksprungkante von Stop zu Start nicht mitgezählt). Im Beispiel ergibt sich M = 11 - 9 + 2 = 4, siehe Abschnitt „Bestimmung der Zyklomatischen Komplexität über Knoten und Kanten des Kontrollflusses“.

5. Was sagt die Zyklomatische Komplexität über die Zahl der nötigen Testfälle aus? Antwort

M ist die Zahl der linear unabhängigen Pfade (Basispfade). So viele Testfälle brauchst Du, um alle Basispfade zu durchlaufen; für eine vollständige Zweigabdeckung reichen höchstens so viele, oft weniger, siehe Abschnitt „Bestimmung der Zyklomatischen Komplexität über die linear unabhängigen Pfade“.

6. Wo liegen die Grenzen der Aussagekraft der Zyklomatischen Komplexität? Antwort

Einfache switch/case-Konstrukte haben eine hohe McCabe-Zahl, obwohl sie leicht verständlich sind. Impliziten Kontrollfluss über Polymorphie, Lambda-Ausdrücke oder Streams erfasst die Metrik nicht. Sie ist daher ein Indiz, aber kein alleiniges Maß für Komplexität, siehe Abschnitt „Aktuelle Aussagekraft der Zyklomatischen Komplexität“.

7. Ab welchen Werten gilt eine Methode als zu komplex? Antwort

Eine allgemeingültige Grenze gibt es nicht. Verbreitet ist: bis 10 gut testbar, 11 bis 20 noch testbar, 21 bis 50 komplex und schwer zu testen, über 50 praktisch nicht testbar. Ab 21 sollte möglichst, über 50 auf jeden Fall refaktorisiert werden, siehe Abschnitt „Einordnung der Werte Zyklomatischer Komplexität“.

Links und weitere Informationen

• Die Zyklomatische Komplexität des Bubblesort-Algorithmus

• Laufzeitkomplexität von Algorithmen und Big-O-Notation

• als Originalquelle: Thomas J. McCabe: „A Complexity Measure“. IEEE Transactions on Software Engineering, SE-2 (4), 1976, S. 308–320

• als Nachschlagewerk: Arthur H. Watson, Thomas J. McCabe: Structured Testing: A Testing Methodology Using the Cyclomatic Complexity Metric (NIST Special Publication 500-235), 1996

Hinweis zur Nachnutzung als Open Educational Resource (OER)

Dieser Artikel und seine Texte, Bilder, Grafiken, Code und sonstiger Inhalt sind - sofern nicht anders angegeben - lizenziert unter CC BY 4.0. Nennung gemäß TULLU-Regel bitte wie folgt: “Metrik der Komplexität eines Algorithmus: Die McCabe-Zahl (Zyklomatische Komplexität)” von oer-informatik.de (H. Stein), Lizenz: CC BY 4.0. Der Artikel wurde unter https://oer-informatik.de/zyklomatische-komplexitaet veröffentlicht, die Quelltexte sind in weiterverarbeitbarer Form verfügbar im Repository unter https://gitlab.com/oer-informatik/algorithmik/algorithmen. Erstellt mit KI-Assistenz; von mir umfassend redaktionell überarbeitet, geprüft und freigegeben. Stand: 23.10.2026.

[Kommentare zum Artikel lesen, schreiben] / [Artikel teilen] / [gitlab-Issue zum Artikel schreiben]