Erweitere Flipflops: D-, T-, JK- und JK-MS-Flipflops
https://bildung.social/@oerinformatik/113781503270131724
https://oer-informatik.de/flipflops_d-t-jk
tl/dr; (ca. 10 min Lesezeit): Eine Reihe von Flipflop-Grundschaltungen wiegen die Nachteile von einfachen RS-Flipflops auf und sind geeignet für besondere Aufgaben: D-Flipflops verfügen neben dem Takt über nur einen Dateneingang, und sind deshalb besonders zum Datenspeichern (in Registern) geeignet, T-Flipflops verfügen nur noch über den Takteingang und eignen sich als Freuquenzteiler oder Zähler, und JK-Flipflops sind die Universalisten, mit denen sehr vieles möglich ist. (Zuletzt geändert am 06.01.2025)
Teil der Serie zu Flipflopschaltungen: Grundlagen, Taktsteuerung, D-/T-/JK-Flipflops
Wir haben in den vorigen Artikeln die Grundlagen von Flipflops und deren Taktsteuerung am Beispiel von RS-Flipflops kennengelernt. Häufig werden jedoch nicht RS-Flipflops selbst verwendet, sondern sie werden zu weiteren Flipflop-Schaltungen kombiniert.
D-Flipflop mit Taktzustandssteuerung
Bei einem D-Flipflop wird der Wert am Eingang D beim Taktzustand C=1 den Ausgang durchgeleitet. Beim Taktzustand C=0 wird der zuletzt eingelesene Zustand ausgegeben und kann erst wieder beim nächsten C=1 geändert werden. Der Name D-Flipflop geht gleichermaßen darauf zurück, dass es Daten speichert und diese noch einen halben Takt lang verzögert (Delay) am Ausgang anliegen.
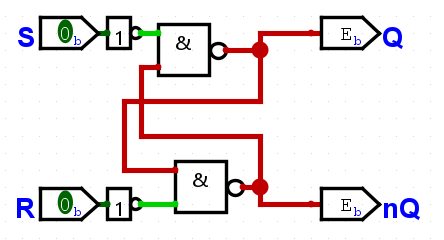
Diese Charakteristik lässt sich mit unterschiedlichen Schaltungen realisieren. Wir machen es uns einmal einfach und nutzen unsere Grundlagen zur Taktsteuerung aus dem vorigen Artikel, denn auf Grundlage eines taktzustandsgesteuerten RS-Flipflops haben D-Flipflops einen sehr einfachen Aufbau: der Reset-Eingang eines RS-Flipflops wird invertiert mit dem Set-Eingang verknüpft, das Taktsignal einfach durchgereicht. Durch diese Schaltung ist auch sichergestellt, das es bei dieser Art Flipflop keinen irregulären Zustand gibt.

Ohne irregulären Zustand gilt hier also in jedem Fall Q_1 = \lnot \overline{Q_2} (also Q_1 = Q_2), wir können hier also bedenkenlos die beide Ausgänge mit Q nzw. \overline{Q} bezeichnen.
Bei Taktzustandsgesteuerten D-Flipflops wird dem taktabhängigen Eingang wieder die Nummer des zugehörigen Takts voran gestellt (1D gehört zu C1), da es sich um Taktzustandssteuerung handelt, wird am Takteingang kein weiteres Symbol notiert:

Die Wertetabelle lässt sich in zwei Sätzen zusammenfassen: Bei einem HIGH-Signal an der Clock entspricht das Ausgangssignal dem Eingangssignal. Bei einem LOW-Signal an der Clock wird der vorige Wert beibehalten.
| Dateneingang D zum Zeitpunkt t |
Clock C Zustand |
Ausgang Q_{t} zum Zeitpunkt t |
Erläuterung |
|---|---|---|---|
| 0 | 1 | 0 | Einlesen bei C=1: Q_t = D_t = 0 |
| x | 0 | D_{t-1} | Wenn C=0: Ausgabe letzter gespeicherter Wert. Aktueller D unerheblich (“x” = don’t care) |
| 1 | 1 | 1 | Einlesen bei (C=1): Q_t = D_t = 1 |
D-Flipflop mit Taktflankensteuerung
D-Flipflops lassen sich auch mit einer Taktflankensteuerung realisieren.
Nehmen wir wieder ein RS-Flipflop aus Grundlage, so ist der Aufbau analog zu dem obigen Aufbau: Das taktzustandsgesteuerte RS-Flipflops wird nur durch ein taktflankengesteuertes RS-Flipflop (siehe voriger Artikel) ersetzt:

Entsprechend ändert sich auch in der Wertetabelle lediglich, dass wir nicht mehr den Zustand der Clock betrachten (also 0 oder 1), sondern unterscheiden, ob an der Clock eine steigende Flanke (\uparrow) auftritt, oder nicht (spricht: 1, fallende Flanke oder 0: \bar{} \downarrow \_).
| Dateneingang D zum Zeitpunkt t |
Clock C Flanken/Zustand |
Ausgang Q_{t} zum Zeitpunkt t |
Erläuterung |
|---|---|---|---|
| 0 | \uparrow | 0 | Einlesen bei steigender Flanke: Q_t = D_t = 0 |
| x | \bar{} \downarrow \_ | D_{t-1} | Wenn keine steigende Flanke an Clock: Ausgabe letzter gespeicherter Wert. Aktueller Wert D unerheblich (“x” = don’t care) |
| 1 | \uparrow | 1 | Einlesen bei steigender Flanke: Q_t = D_t = 1 |
Im Schaltzeichen von taktflankengesteuerten D-Flipflops erscheint wieder das “Flankendreieck” am Takteingang:

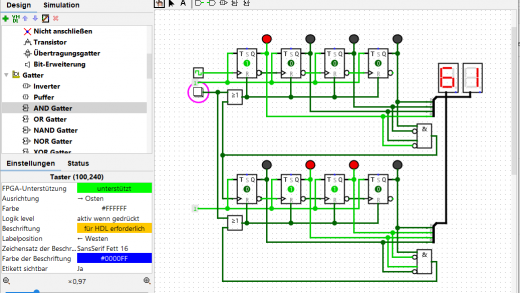
In der Praxis werden D-Flipflops vor allem zum Speichern von Daten in Registern verwendet. Hierbei wird genutzt, dass jedes D-Flipflop den aktuellen Wert mit jedem Takt am Ausgang weiterschiebt. Seriell verknüpfte D-Flipflops bauen also Schieberegister auf, die mehrere Bit speichern können - im folgenden Beispiel sind dies vier Bit, die mit vier Taktzyklen hinein (und heraus) geschoben werden. Man erkennt schön, wie jedes Datenbit mit Verzögerung von D-Flipflop zu D-Flipflop geschoben wird:

T-Flipflop
Eine weitere Flipflop-Schaltung mit ähnlich einfacher Funktion ist das T-Flipflop: dieses Flipflop besitzt lediglich einen Eingang (T) und wechselt den Zustand am Ausgang Q mit jeder steigenden Flanke an diesem Eingang. Dieser Zustandswechsel am wird aus dem Englischen togglen genannt, was dem Flipflop den Namen gibt.
Aufgebaut werden kann diese Funktionalität beispielsweise, indem der negierte Ausgang eines taktgesteuerten D-Flipflops an den Daten-Eingang zurückgeführt wird:

Im Gegensatz zu den anderen Flipflops ergibt es keinen Sinn, ein “toggelndes” Flipflop mit einem zustandsgesteuerten Eingang zu belegen - bei einem HIGH-Signal an T würde es unentwegt oszillieren (den Zustand wechseln). Daher gibt es dieses Flipflop nur in einer flankengesteuerten Variante. Das Schaltzeichen zeigt dies wiederum durch das Dreieck am Eingang T an:

Die Wertetabelle ist noch einfacher aufgebaut, als die des D-Flipflops: Bei einer anliegenden steigende Flanke (\uparrow) wechselt der Zustand am Ausgang von 0 auf 1 bzw. umgekehrt (Q_t = \overline{Q_{t-1}}), bei allen anderen Zuständen und fallenden Flanken (spricht: an T liegt 1, fallende Flanke oder 0 an: \bar{} \downarrow \_) bleibt der Ausgang unverändert (Q_t = Q_{t-1}).
| Dateneingang T zum Zeitpunkt t |
Ausgang Q_{t} zum Zeitpunkt t |
Erläuterung |
|---|---|---|
| \uparrow | \overline{Q_{t-1}} | Toggeln (Zustandswechsel) bei steigender Flanke: Q_t = \overline{Q_{t-1}} |
| \bar{} \downarrow \_ | Q_{t-1} | Wenn keine steigende Flanke Ausgabe letzter gespeicherter Wert. |
Da T-Flipflops am Ausgang mit halbierter Frequenz zum Eingangssignal den Zustand wechseln, finden sie vor allem in Frequenzteilern oder binären Zählern Verwendung. Hierzu wird der negierte Ausgang des einen mit dem Eingang des folgenden T-Flipflops verbunden:

Man erkennt deutlich, dass die roten Signale von Flipflop zu Flipflop mit halber Frequenz leuchten. Gut erkennen lässt sich dieses Verhalten auch am Impulsdiagramm eines solchen Frequenzteilers / Binärzählers:

Auch beim T-Flipflop sind natürlich alle bekannten Erweiterungen denkbar, wie wir sie bereits beim RS-Flipflop kennengelernt haben: Zweiflankensteuerung, taktunabhängige Eingänge. Aufbau und Verhalten gleichen dem des RS-Flipflops und werden beim JK-Flipflop nochmals dargestellt - so dass wir uns Details hierzu sparen. Bei der Zweiflankensteuerung wird wieder das Ausgangssignal des Haupt-Flipflops durch ein zweites RS-Flipflop mit einem invertierten Taktsignal verzögert (fallende Taktflanke) ausgegeben, was man an der angedeuteten Taktflanke am Ausgang erkennen kann:

Die Flipflop-Königsklasse: das JK-Flipflop
Ein RS-Flipflop mit zwei binären Eingängen könnte auf Viererlei (2^2 = 4) unterschiedliche Arten auf Eingangssignale reagieren. Wir nutzen jedoch lediglich drei Varianten: Setzen, Rücksetzen und Speichern. Die Eingangskombination (R=1, S=1) verhält sich irregulär und sollte gemieden werden: je nach internem Aufbau des RS-Flipflops sind beide Ausgänge (Q, \overline{Q}) HIGH oder LOW - und damit nicht wie eigentlich gewünscht gegensätzlich. Oder aber die interne Schaltung dupliziert durch Dominanz-Schaltung das Verhalten einer anderen Kombination (z.B. bei Setzdominanz:(R=1, $S=19 verhält sich wie (R=0$, S=1) ). Wir verschenken also eine von vier Verhaltensvarianten des Flipflops.
Dieses Problem adressiert das JK-Flipflop: es verhält sich in drei Eingangskombinationen wie ein RS-Flipflop (Setzen, Rücksetzen und Speichern), an Stelle des irregulären Zustands des RS-Flipflops (wenn also beide Eingänge 1 sind) bietet es aber zusätzlich toggelndes Verhalten, wie wir das beim T-Flipflop kennengelernt haben.
Die Wertetabelle eines JK-Flipflops sieht also folgendermaßen aus:
| Jump J (\widehat{=} Set) zum Zeitpunkt t |
Kill K (\widehat{=} Reset) zum Zeitpunkt t |
Clock C Flanken/Zustand |
Ausgang Q_{t} zum Zeitpunkt t |
Erläuterung |
|---|---|---|---|---|
| x | x | \bar{} \downarrow \_ | Q_{t-1} | Wenn keine steigende Flanke Ausgabe letzter gespeicherter Wert. Aktueller Werte J und K unerheblich (“x” = don’t care) |
| 0 | 0 | \uparrow | Q_{t-1} | Speichern Q_t = Q_{t-1} |
| 0 | 1 | \uparrow | 0 | Kill: Rücksetzen bei steigender Flanke: Q_t = 0 |
| 1 | 0 | \uparrow | 1 | Jump: Setzen bei steigender Flanke: Q_t = 1 |
| 1 | 1 | \uparrow | \overline{Q_{t-1}} | Toggeln (Zustandswechsel) bei steigender Flanke: Q_t = \overline{Q_{t-1}} |
Erreicht wird dieses toggelnde Verhalten beispielsweise, in dem bei einem RS-Flipflop eine zusätzliche Rückkopplung zum gegengleichen Ausgang ergänzt wird. Es gibt natürlich viele weitere Wege, wie das Flipflop aufgebaut werden kann - dies ist nur eine Variante, die auf von uns besprochenen Grundkomponenten beruht.
Damit es zu keiner Verwechslung mit den Eingängen eines RS-Flipflops kommt, werden die Eingänge mit J (für Jump, entspricht Set) und K (für Kill, entspricht Reset) bezeichnet.

Da JK-Flipflops wie auch T-Flipflops über toggelndes Verhalten verfügen, ergibt eine Taktzustandssteuerung auch hier wenig Sinn. Beim Taktzustand C=1 und (R=1, S=1) würde sonst das Flipflop unentwegt toggeln.Die Flipflops verfügen also über eine Flankensteuerung, was mit dem Flankendreieck am Takteingang des Schaltzeichens symbolisiert wird.

Übungsaufgabe
JK-Flipflops sind vor allem deshalb beliebt, weil sie sehr flexibel verschaltet werden können. Mit wenigen Grundgattern und HIGH und LOW-Potenzial sind schnell viele Grundschaltungen aufgebaut. Erstelle eine Schaltung, die mit Hilfe von JK-Flipflops:
die Funktionalität eines T-Flipflops aufweist,
die Funktionalität eines D-Flipflops aufweist,
die Funktionalität eines RS-Flipflops mit dominantem Setzen aufweist.
JK-MS-Flipflop
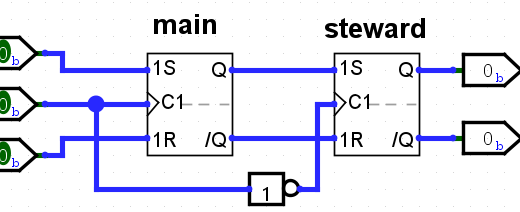
Wie bei RS- und T-Flipflops können auch JK-Flipflops um eine Zweitaktflankensteuerung erweitert werden: das erste Haupt-Flipflop (main / früher: master) nimmt das Signal bei der steigenden Taktflanke entgegen und reicht es an die Eingänge eines zweiten (steward / früher: slave) weiter. Das zweite Flipflop gibt die Signale wiederum bei der sinkenden Tankflanke an den Ausgang weiter. Diese Art Flipflop wird als MS-Flipflop oder zweitaktflankengesteuertes Flipflop bezeichnet.

Durch dieses Verfahren ist sichergestellt, dass sich während der Signalverarbeitung eines Takts keine Eingangszustände mehr ändern.
Die Ausgabe bei fallender Taktflanke wird wieder durch die symbolisierte fallende Taktflanke am Ausgang symbolisiert:

Die beiden Flipflops eines JK-MS-Flipflops schalten immer mit einem halben Takt Verzögerung. Betrachten wir das Impulsdiagramm eines 4-Bit-Synchronzählers, so können wir die Verzögerung gut im Diagramm erkennen. Dieser Zähler ist aus vier JK-MS-Flipflops aufgebaut:

Im zugehörigen Impulsdiagramm ist jeweils die weitergabe des Zustands der verarbeitenden main-Flipflops (Q_xm) an das ausgebende steward-Flipflop (Q_xs) mit Pfeilen hervorgehoben:

JK-MS-Flipflop mit taktunabhängigen Eingängen (Preset/Clear)
Alle Varianten des JK-Flipflops lassen sich durch taktunabhängige Eingänge erweitern. Wie schon beim RS-Flipflop werden diese häufig als Preset (taktunabhängiges Setzen) und Clear (taktunabhängiges Rücksetzen) bezeichnet.
Um den internen Aufbau nicht zu komplex erscheinen zu lassen, referenziere ich hier direkt auf das taktflankengesteuerte RS-Flipflop mit Preset und Clear: zwei davon werden benötigt, um ein JK-MS-Flipflop mit Preset und Clear zu erstellen.

In diesem Beispiel wurden sowohl Preset als auch Clear HIGH-aktiv ausgeführt, d.h., um taktunabhängig zurückzusetzen muss ein HIGH an PRE angelegt werden. Ein Schaltzeichen für diese Art Flipflop würde so aussehen:

Realisiert werden diese Schaltungen jedoch zumeist LOW-aktiv, d.h. ein Pin mit der Bezeichnung \overline{PRE} wird nach außen geführt, der auf LOW gelegt werden muss, um taktunabhängig zurückzusetzen und im normalen Betrieb gegen HIGH verdrahtet sein sollte.
JK-MS-Flipflops kommen in zahllosen Schaltungen zur Anwendungen, wir werden sie uns im Folgenden u.a. beim Zähleraufbau nochmals genauer ansehen. Neben den Binärzählern, die wir oben bereits kurz gesehen hatten, können beliebige andere Zählcodes mithilfe von Flipflopschaltungen erzeugt werden. Als kleiner Vorgeschmack hier eine synchrone Zählschaltung, die mit dem Graycode von 0 bis 9 zählt:

Übungsaufgaben
Das war so ziemlich alles, was man zum Aufbau von einfachen Flipflops wissen muss. Wer halbwegs verstanden hat, welche Funktionen die jeweiligen Flipflops haben, welche Ansteuerungen es gibt, und wie sie sich unterscheiden, der sollte die folgenden beiden Impulsdiagramme problemlos vervollständigen können:


Hinweis: In den roten Bereichen befindet sich das Flipflop im irregulären Zustand - ohne konkrete Information über den internen Aufbau ist keine Aussage möglich ob die Ausgänge HIGH oder LOW sind.


Links und weitere Informationen
Die Beispieldatei mit den aufgebauten Flipflopschaltungen (in der Software Logisim Evolution) findet sich hier (link)
Hinweis zur Nachnutzung als Open Educational Resource (OER)
Dieser Artikel und seine Texte, Bilder, Grafiken, Code und sonstiger Inhalt sind - sofern nicht anders angegeben - lizenziert unter CC BY 4.0. Nennung gemäß TULLU-Regel bitte wie folgt: “Erweitere Flipflops: D-, T-, JK- und JK-MS-Flipflops” von oer-informatik.de (H. Stein), Lizenz: CC BY 4.0. Der Artikel wurde unter https://oer-informatik.de/flipflops_d-t-jk veröffentlicht, die Quelltexte sind in weiterverarbeitbarer Form verfügbar im Repository unter https://gitlab.com/oer-informatik/digitaltechnik. Stand: 06.01.2025.
[Kommentare zum Artikel lesen, schreiben] / [Artikel teilen] / [gitlab-Issue zum Artikel schreiben]