Einfache Speicherschaltungen mit Flipflops

Grundlagen der Speicherschaltungen

https://bildung.social/@oerinformatik/113759935521348297

https://oer-informatik.de/flipflops

tl/dr; (ca. 9 min Lesezeit): Neben einfachen Logikschaltungen sind Speicherschaltungen die wesentliche Grundlage der Informationstechnik. Flipflops lassen sich einfach aus NAND und NOR aufbauen, verfügen über einen irregulären Zustand, den man über Setz- und Rücksetzdominanz umgehen kann. Aus der Namensgebung (RS/SR) lässt sich leider nicht einheitlich auf die Funktion schließen, da dies unterschiedlich gehandhabt wird. Kleine Übungsaufgaben sind in den Text integriert. (Zuletzt geändert am 06.01.2025)

Teil der Serie zu Flipflopschaltungen: Grundlagen, Taktsteuerung, D-/T-/JK-Flipflops

Eine der wichtigsten Grundschaltungen aus Logikgatter sind Speicherschaltungen, die stabile Zustände auch nach dem eigentlichen Schaltvorgang behalten. Aufgrund der Geräusche, die diese Schaltvorgänge gemacht hatten, nennt man sie seltener “bistabile Kippstufe” und häufiger einfach: Flipflop. Es gibt neben dem einfachen RS-Flipflop auch noch taktgesteuerte oder kombinierte Flipflopschaltungen bis hin zum MS-JK-Flipflop werden hier alle Grundschaltungen vorgestellt

RS-Flipflop aus NOR-Gattern

Die einfachste Speicherschaltung erhält man, in dem man zwei NOR-Gatter kombiniert und die Ausgänge wechselseitig an die Eingänge des anderen zurückführt. Das so entstandene Logikgatter kann zwei Zustände (0 und 1) speichern: eine bistabile Kippstufe. Deutlich verbreiteter als die Bezeichnung bistabile Kippstufe ist aber die lautmalerische Bezeichnung: Flipflop. Dieses erste einfache Flipflop hat einen Eingang S (für set). Liegt an S ein HIGH-Signal an, wird der Zustand am Ausgang (Q) auf HIGH gesetzt. Der Ausgang speichert diesen Zustand auch, wenn S wieder auf LOW gewechselt hat. Erst wenn an einem zweiten Eingang R (für reset) ein HIGH anliegt, wechselt der Ausgang Q wieder auf LOW. Aufgrund der Eingänge Reset und Set wird diese Schaltung als “RS-Flipflop” bezeichnet.

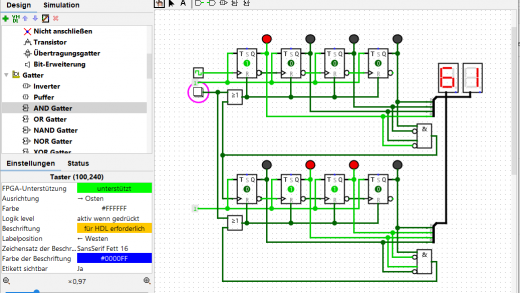
Ein Aufbau zum selbst ausprobieren findet sich hier bei der WebApp LogiJS.

In Logik-Schaltplänen wird ein RS-Flipflop als eigenes Schaltzeichen dargestellt:

Schaltzeichen eines RS-Flipflops auf NOR-Basis — Schaltzeichen eines RS-Flipflops auf `NOR`-Basis

Der irreguläre Zustand ( S=1 und R=1 )

RS-Flipflops verfügen neben dem Ausgang Q auch über einen zweiten Ausgang, der i.d.R. ein zu Q negiertes Signal ausgibt. Dieser wird daher als “nicht Q” (geschrieben: \overline{Q}) bezeichnet.

Bei der obigen Simulation zeigt sich jedoch, dass nicht in jedem Fall am Ausgang \overline{Q} das negierte Signal von Q anliegt: Für den Fall, dass die Eingänge mit S =1 und R =1 belegt sind, stellt sich an beiden Ausgängen 0 (LOW) ein: sowohl Q = 0 als auch \overline{Q} = 0.

Es ist also für diesen Fall schaltalgebraisch falsch, die beiden Ausgänge Q und \overline{Q} zu nennen. Daher nennt man diesen Zustand (S = 1, R = 1) den irregulären Zustand. In der Literatur werden die beiden Ausgänge oft mit unterschiedlichen Suffixen belegt, um in der Benamung konsistent zu bleiben: Q \ \widehat{=} \ Q_1 und \overline{Q} \ \widehat{=} \ \overline{Q_2}.

Nicht immer ist der “Überstrich” verfügbar (\overline{Q_2}), daher wir die Negierung oft durch den logischen nicht-Operator (\neg{Q_2}), ein Ausrufezeichen (!Q_2), den Schrägstrich (/Q_2) oder (und jetzt folgen die unschönen Varianten) ein vorangestelltes “n” (nQ_2) oder Minus (-Q_2) ersetzt.

Im Ganzen zeigt das Flipflop also vier verschiedene Verhaltensweisen:

Setzen: der Ausgang Q_{1} wird von 0 auf 1 gesetzt.
Rücksetzen: der Ausgang Q_{1} wird von 1 auf 0 gesetzt.
Speichern: der Ausgang Q_{1} zum aktuellen Zeitpunkt (t) behält den Wert, den er bereits zum vorigen Zeitpunkt (t-1) hatte: Q_{1}(t) = Q_{1}(t-1)
irregulärer Zustand: Beide Ausgänge (Q_1, \overline{Q_2}) haben den gleichen Zustand (bei NOR-Flipflops: 0).

Wertetabelle eines NOR-RS-Flipflops
Reset R	Set S	Ausgang Q_1 nach dem Schalten Q_{1}(t)	Ausgang \overline{Q_2} nach dem Schalten \overline{Q_{2}(t)}	Funktion
0	0	Q_{1}(t-1)	\overline{Q_{2}(t-1)}	Speichern
0	1	1	0	Setzen
1	0	0	1	Rücksetzen
1	1	0	0	irregulärer Zustand

RS-Flipflop aus NAND-Gattern - und der andere irreguläre Zustand

RS-Flipflops lassen sich nicht nur mit NOR, sondern auch mit zwei NAND-Gattern aufbauen. Auch hier werden die Ausgänge wechselseitig zum jeweils anderen NAND-Gatter geführt. Werden lediglich zwei NAND-Gatter verbaut, verhält sich das Flipflop anders, als das NOR-Flipflop: Geschaltet wird, wenn die Eingänge auf LOW wechseln (wir haben also \overline{S} und \overline{R}-Eingänge, die Eingänge sind low-active).

Ein RS-Flipflop aus NAND-Gattern - mit low-aktiven Eingangssignalen

Damit wir auch hier wieder einen Set und einen Reset-Eingang erhalten, müssen wir noch zwei NOT-Gatter (Invertierer) vor die Eingangssignale schalten, dann sieht das Ergebnis schon fast aus, wie beim NOR-Flipflop:

Auch mit diesen Anpassungen verhält sich das NAND-Flipflop etwas anders, als das NOR-Flipflop oben: im irregulären Zustand (also wenn beide Eingänge HIGH sind) sind die Ausgänge Q_1 = 1 als auch \overline{Q_2} = 1. Beim Flipflop aus NOR-Gattern waren beide Ausgänge 0 (also LOW).

Wertetabelle eines NAND-RS-Flipflops
Reset R	Set S	Ausgang Q_1 nach dem Schalten Q_{1}(t)	Ausgang \overline{Q_2} nach dem Schalten \overline{Q_{2}(t)}	Funktion
0	0	Q_{1}(t-1)	\overline{Q_{2}(t-1)}	Speichern
0	1	1	0	Setzen
1	0	0	1	Rücksetzen
1	1	1	1	irregulärer Zustand

Auch für das NAND-Gatter gibt es zum Spielen eine Simulation bei LogiJS (link).

Zur Unterscheidung von NOR- und NAND-Flipflops werden bei NAND-Flipflops in Schaltzeichen häufig die negierten Eingänge (\overline{S},\overline{R}) negiert ausgeführt, so dass sich durch doppelte Negierung zwar R- und S-Eingänge ergeben, aber deutlich wird, dass das Flipflop den charakteristischen irregulären Zustand eines NAND-Flipflops zeigt.

Schaltzeichen eines RS-Flipflops auf NAND-Basis — Schaltzeichen eines RS-Flipflops auf `NAND`-Basis

Allgemeine Wertetabelle für RS-Flipflops

Der Zustand am Ausgang Q des Flipflops zum Zeitpunkt t hängt ab:

von den beiden Eingangssignalen Set und Reset,
vom Wert am Ausgang Q vor dem letzten Schaltvorgang (Q(t-1))
und vom internen Aufbau: Wenn sowohl S als auch R aktiv (HIGH) sind reagiert ein NOR-Flipflop anders als ein NAND-Flipflop.

Sofern wir keine Informationen über den internen Aufbau haben, sollten wir diesen irregulären Zustand meiden. Manche bezeichnen ihn daher als den verbotenen Zustand. Wir vereinfachen und betrachten diesen Zustand als unbestimmt. Eine allgemeine Wertetabelle für ein RS-Flipflop, dessen internen Aufbau wir nicht kennen (NAND oder NOR) mit den Eingangssignalen S und R und dem Ausgangssignal Q können wir also so notieren:

Wertetabelle aller möglicher Zustände eines RS-Flipflops
Reset R	Set S	Ausgang Q_{1} nach dem Schalten Q_{1}(t))	Ausgang \overline{Q_{2}} nach dem Schalten \overline{Q_{2}(t)})	Funktion
0	0	Q_{1}(t-1)	\overline{Q_{2}(t-1)}	Speichern
0	1	1	0	Setzen
1	0	0	1	Rücksetzen
1	1	unbestimmt	unbestimmt	irregulärer Zustand

Wir können den Zustand vor dem Schalten (Q(t-1)) als zusätzlichen Eingabewert verstehen und somit in die Wertetabelle aufnehmen - allerdings wird die Darstellung dann etwas unübersichtlicher. Wenn wir alle Kombinationen an Eingangssignalen aufzeichnen, können wir die Bereiche kennzeichnen, in denen das Setzen und Rücksetzen des Flipflops keine Zustandsänderung bewirkt, da der jeweilige Zustand bereits vorhanden war: ich habe diese Zeilen mit no op gekennzeichnet (was der Name eines Maschinenbefehls ist, der nichts bewirkt).

Wertetabelle aller möglicher Zustände eines RS-Flipflops
Reset R	Set S	Ausgang Q vor dem Schalten Q(t-1)	Ausgang Q nach dem Schalten Q(t)	Funktion
0	0	0	0 ( = Q(t-1))	Speichern
0	0	1	1 ( = Q(t-1))	Speichern
0	1	0	1	Setzen
0	1	1	1	Setzen (no op)
1	0	0	0	Rücksetzen (no op)
1	0	1	0	Rücksetzen
1	1	0	*unbestimmt*	irregulärer Zustand
1	1	1	*unbestimmt*	irregulärer Zustand

Abfolge der Schaltvorgänge im Impulsdiagramm

Eine konkrete Schaltabfolge könnte im Impulsdiagramm folgendermaßen aussehen. Wir gehen davon aus, dass zu Beginn nicht definiert ist, welchen Zustand das Flipflop hat (üblicherweise ist der Ausgangszustand von Flipflops definiert mit Q = 0):

Schaltabfolge eines Impulsdiagramms

Das Flipflop hat nach dem Einschalten zunächst einen undefinierten Zustand, dieser muss durch Rücksetzen auf Q = 0 (in der Grafik bei 0,5s) gesetzt werden. Im Folgenden wird zweimal das Set-Signale gesendet - wobei nur beim ersten mal (nach 1,5s) eine Zustandsänderung am Ausgang auf Q = 1 erfolgt (das zweite Setzen ist mit no op und grau markiert, da es keine Zustandsänderung bewirkt - ebenso ab Sekunde 6,5, wo erneutes Rücksetzen keine Änderung bewirkt).

Nach dem gleichzeitigen Betätigen von R und S ab Sekunde 4,5 ist wieder nicht definiert, welchen Zustand das Flipflop einnimmt (ein NOR-Flipflop verhält sich hier anders als ein NAND-Flipflop). Dieser Bereich ist daher gelb markiert.

Die Schaltfolge als Wertetabelle dargestellt sieht folgendermaßen aus:

Eine Wertetabelle, die nicht alle möglichen, sondern die im Diagramm dargestellten Zustände chronologisch darstellt
Reset R	Set S	vor dem Schalten Q_{t-1}	nach dem Schalten Q_{t}
0	0	unbestimmt	unbestimmt
1	0	unbestimmt	0
0	0	0	0
0	1	0	1
0	0	1	1
0	1	1	1
0	0	1	1
1	0	1	0
0	0	0	0
1	1	0	unbestimmt
0	0	unbestimmt	unbestimmt
…	…	…	…

Was ist Setz- und Rücksetzdominanz?

Wenn S und R gleichzeitig 1 sind, verhält sich ein NOR-Flipflop rücksetzdominant (Q= 0), ein NAND-Flipflop verhält sich dann setzdominant (Q= 1).

Jedoch verstoßen beide Flipflops gegen die Regel, dass die beiden Ausgänge jederzeit gegensätzliche Ausgangssignale einnehmen ( Q = \neg \overline{Q}).

Wie aber müsste eine Schaltung aussehen, die sicherstellt, dass bei dem RS-Flipflop nie zeitgleich R und S den Wert 1 haben dürfen?

Für ein rücksetzdominantes Flipflop darf am Eingang Set nur dann eine 1 anliegen, wenn an Reset eine 0 anliegt. Das lässt sich mit wenigen Logikgattern umsetzen - am besten probierst Du es direkt ersteinmal selbst:

Übungsaufgabe: Ergänze vor den Eingängen dieses RS-Flipflops (link zu LogiJS) eine Schaltung, die folgende Logik umsetzt:

Ist nur der Taster Set betätigt, so soll das RS-Flipflop am Ausgang Q 1, am Ausgang \overline{Q} 0 sein.
Ist nur der Taster Reset betätigt, so soll das RS-Flipflop am Ausgang Q 0, am Ausgang \overline{Q} 1 sein.
Sind beide Taster (Set und Reset) betätigt, so soll nur das Reset-Signal an das RS-Flipflop durchgereicht werden. Am Ausgang Q soll also eine 0, am Ausgang \overline{Q} eine 1 anliegen.

Aufgabe: erstelle Verriegelungsschaltung für R-dominantes FF

Verriegelungsschaltung für R-dominantes FF

Eine Beispiellösung in LogiJS findet sich über diesen Link (click!)

Für ein setzdominantes Flipflop darf am Eingang Reset nur dann eine 1 anliegen, wenn an Set eine 0 anliegt. Dazu ist jetzt nur noch wenig Transfer nötig - probiere es am Besten wieder selbst aus:

Übungsaufgabe: Ergänze vor den Eingängen dieses RS-Flipflops (link zu LogiJS) eine Schaltung, die folgende Logik umsetzt:

Ist nur der Taster Set betätigt, so soll das RS-Flipflop am Ausgang Q 1, am Ausgang \overline{Q} 0 sein.
Ist nur der Taster Reset betätigt, so soll das RS-Flipflop am Ausgang Q 0, am Ausgang \overline{Q} 1 sein.
Sind beide Taster (Set und Reset) betätigt, so soll nur das Set-Signal an das RS-Flipflop durchgereicht werden. Am Ausgang Q soll also eine 1, am Ausgang \overline{Q} eine 0 anliegen.

Aufgabe: Erstelle Verriegelungsschaltung für S-dominantes FF

Eine Beispiellösung in LogiJS findet sich über diesen Link (click!)

Babylonische Namensverwirrung: RS-Flipflop oder SR-Flipflop?

Ich habe bislang immer von einem “RS-Flipflop” gesprochen - und in der Elektronik ist auch häufig die Reihenfolge R...S geläufig. In der Welt der speicherprogrammierten Steuerungen (SPS) ist die Reihenfolge aber von entscheidender Bedeutung, um die Schaltdominanz abzulesen. Eigentlich ist es ganz einfach: die Norm IEC 61131 legt fest, dass der zuerst genannte Buchstabe die Dominanz vorgibt: ein RS-Flipflop wäre demnach rücksetzdominant, würde also bei (R=1, S=1) den Ausgang auf Q=0 rücksetzen. Um das zu verdeutlichen, wird an den jeweiligen dominanten Eingang eine “1” angehängt (also z.B. R1, das hat aber nichts zu tun mit der Zuordnung zu Taktsignalen, die wir in der Elektronik im nächsten Artikel kennen lernen!).

Nur leider wird hier nicht einheitlich vorgegangen: Siemens (Step7, TIA, Logo) baut die Nomenklatur nach der Schaltsequenz auf: ein RS-Flipflop bei Siemens-S7 würde bei (R=1, S=1) erst Rücksetzen, dann Setzen - am Ende also bliebe gesetzt - damit ist die Verwirrung komplett, denn das Verhalten ist genau gegensätzlich zur Norm.

Take-home-Message zu Flipflop-Schaltdominanz in der SPS-Welt: Immer die jeweilige Dominanz der genutzten SPS-Sprache überprüfen, bevor mit dem Schaltungsdesign begonnen wird, sonst kann es zu bösen Überraschungen kommen!

Nächster Artikel: Taktgesteuerte Flipflops

Bis hierhin waren es nur die Grundaufbauten einfacher Flipflops, mit diesem Handwerkszeug können wir uns auf den nächsten Artikel stürzen:

Taktgesteuerte Flipflops

Links und weitere Informationen

Eine sehr gute und ausführliche Einführung in die Welt der Flipflops findet sich auf elektroniktutor.de
Natürlich führt auch am Elektronik-Kompendium kein Weg vorbei, wenn man sich eingehend mit Flipflops auseinandersetzen will
Die Beispieldatei mit den aufgebauten Flipflopschaltungen (in der Software Logisim Evolution) findet sich hier (link)

Hinweis zur Nachnutzung als Open Educational Resource (OER)

Dieser Artikel und seine Texte, Bilder, Grafiken, Code und sonstiger Inhalt sind - sofern nicht anders angegeben - lizenziert unter CC BY 4.0. Nennung gemäß TULLU-Regel bitte wie folgt: “Grundlagen der Speicherschaltungen” von oer-informatik.de (H. Stein), Lizenz: CC BY 4.0. Der Artikel wurde unter https://oer-informatik.de/flipflops veröffentlicht, die Quelltexte sind in weiterverarbeitbarer Form verfügbar im Repository unter https://gitlab.com/oer-informatik/digitaltechnik. Stand: 06.01.2025.

[Kommentare zum Artikel lesen, schreiben] / [Artikel teilen] / [gitlab-Issue zum Artikel schreiben]